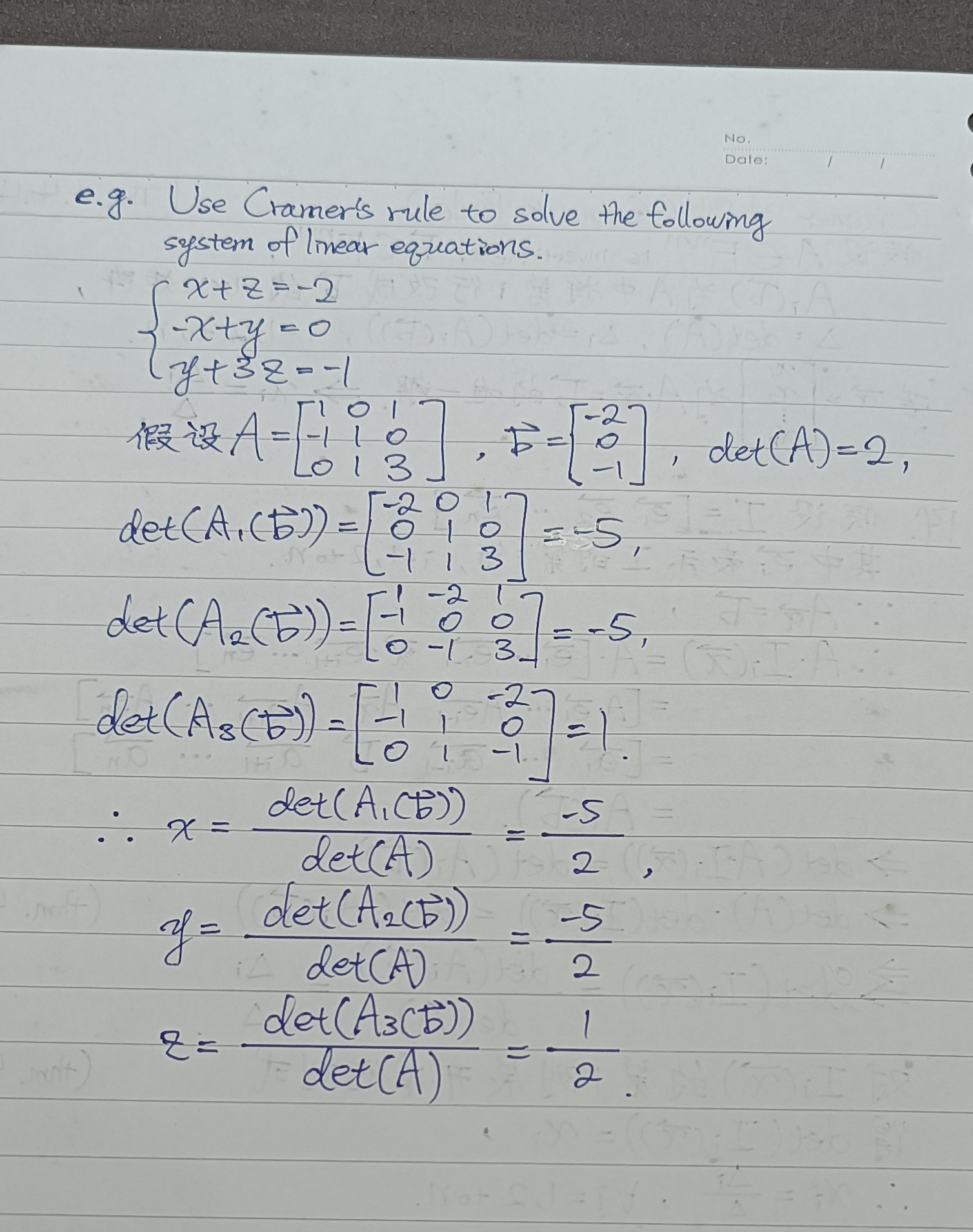章 第01 向量空间
def 1.1 向量空间

def 1.1 eg

def 1.1 notice


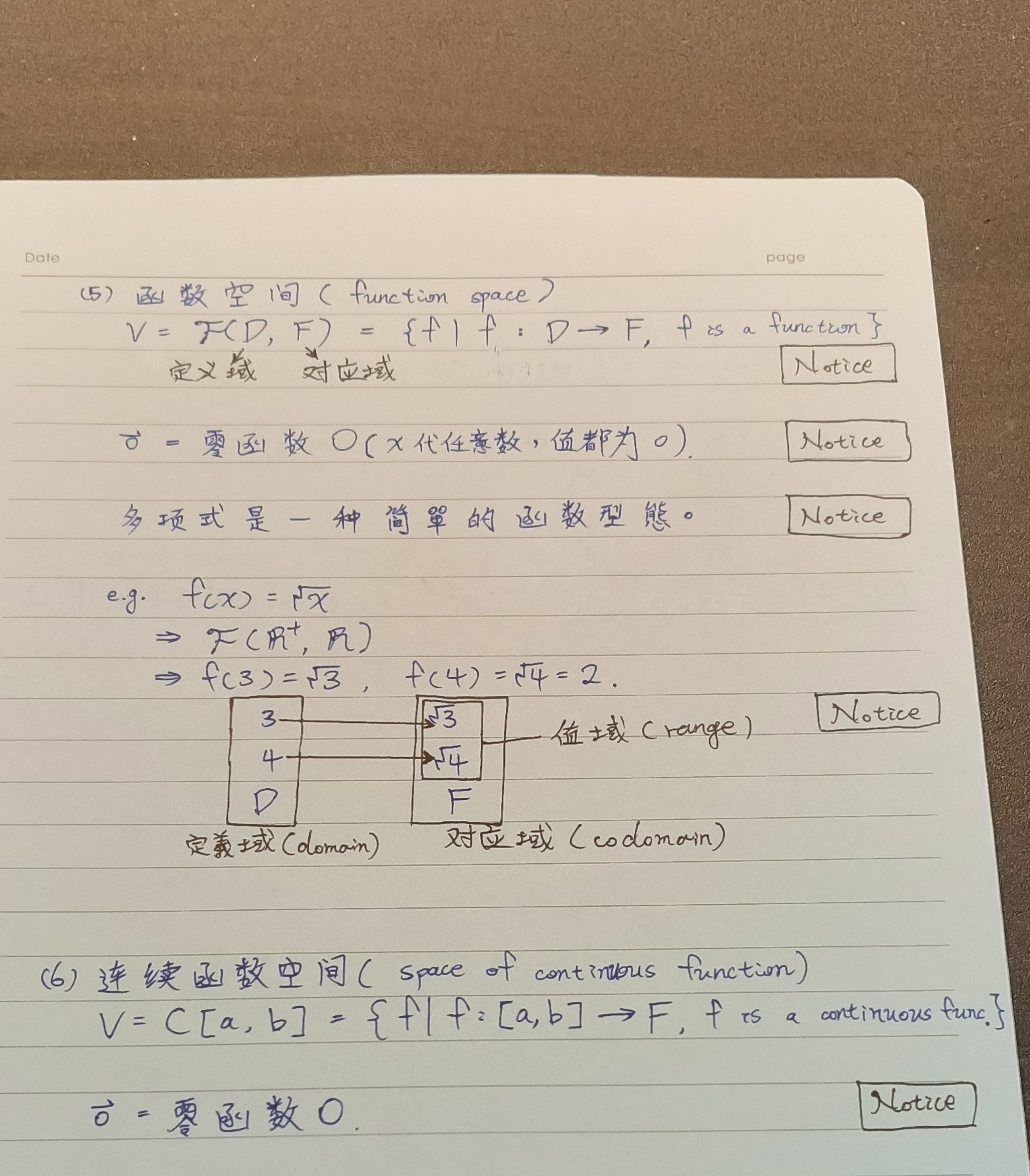
def 1.1 ps



thm 1.1.1
thm 1.1.1 cor 1

thm 1.1.1 cor 2

thm 1.1.2

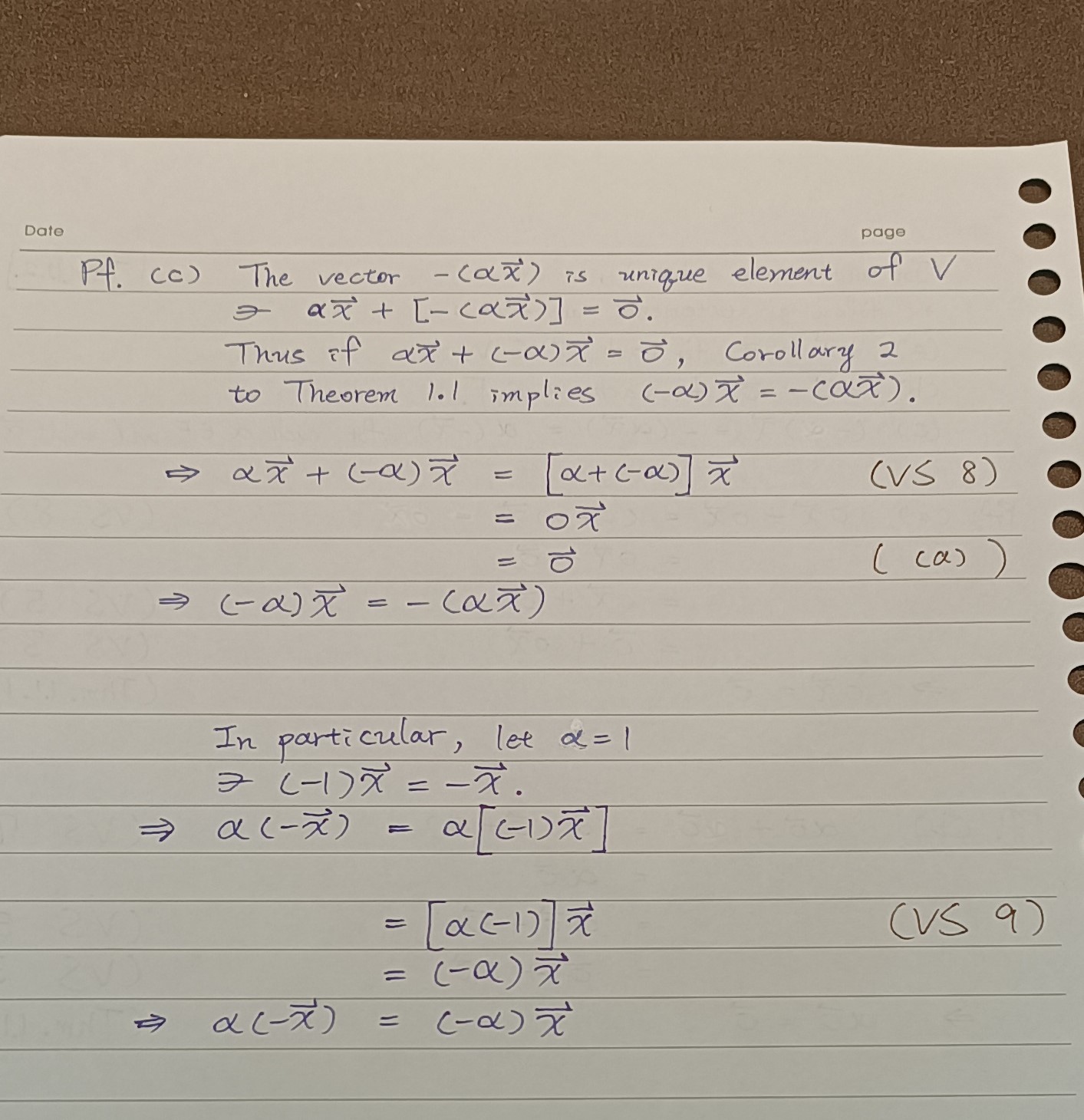
thm 1.1.2 cor 1

def 1.2 子空间
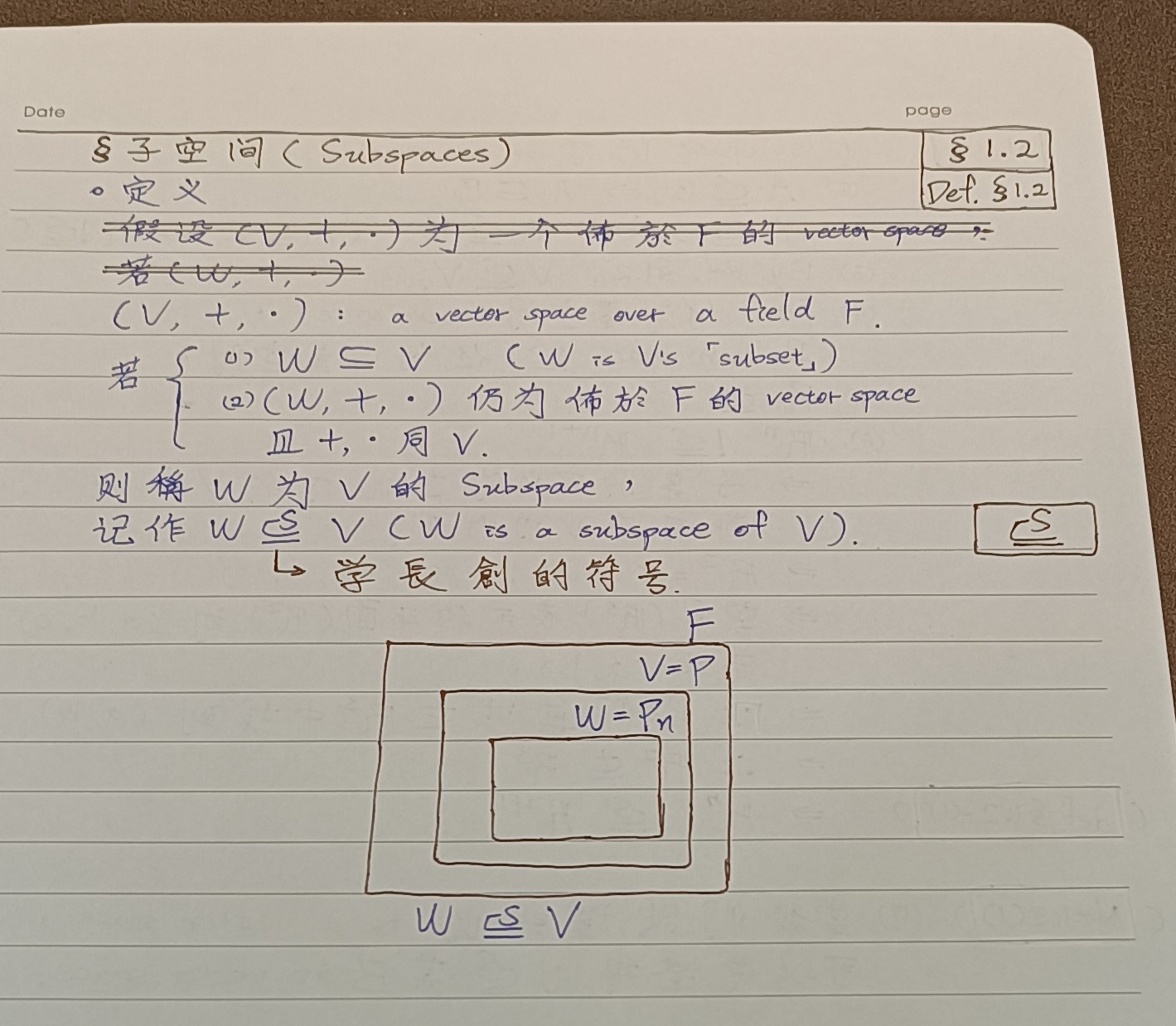
def 1.2 notice


thm 1.2.1



thm 1.2.2


thm 1.2.3

thm 1.2.4

thm 1.2.5

def 1.2.1 和空间(sum space)

thm 1.2.6

def 1.2.2 一个线性映射造出的四个欧氏空间

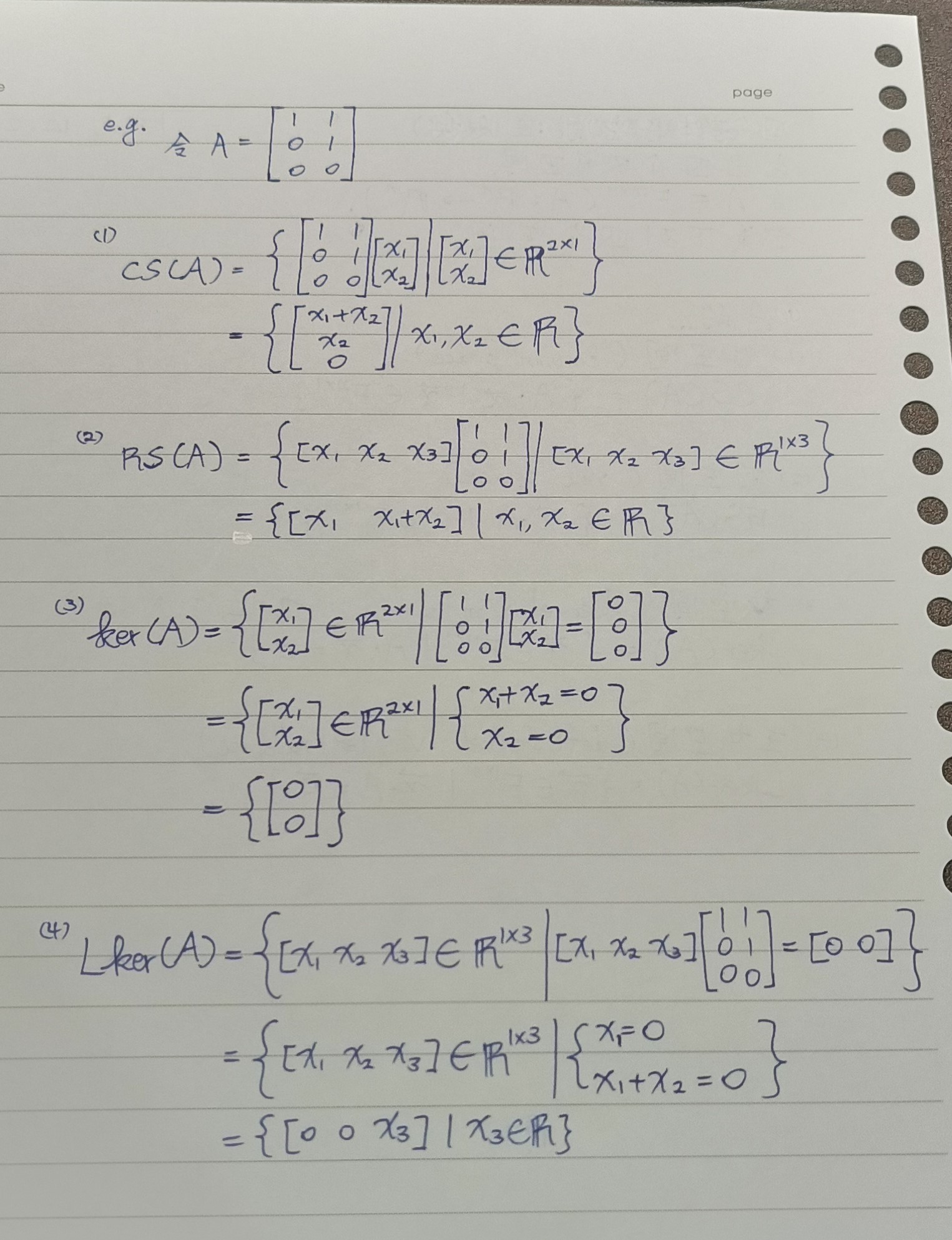
thm 1.2.7


thm 1.2.8

thm 1.2.9

notice 1.2.8, 1.2.9

def 1.3.1 线性组合(linear combination)



def 1.3.2 生成空间(span)


thm 1.3.1


def 1.3.3 生成集(spanning set)

thm 1.3.2



thm 1.3.3

thm 1.3.3 cor 1
def 1.3.4 线性相依集(l.d.s.)、线性独立集(l.i.s.)



def 1.4.1 基底(basis)与维度(dimension)




thm 1.4.1

thm 1.4.2
thm 1.4.3

thm 1.4.4

lemma 1.4.1

thm 1.4.5

thm 1.4.6
def 1.4.2 最小生成集、最大独立集

thm 1.4.7

thm 1.4.8

thm 1.4.9

thm 1.4.10


thm 1.4.11


def 1.5.1 独立子空间(independent subspace)

thm 1.5.1

thm 1.5.2

def 1.5.2 直和(direct sum)

thm 1.5.3

thm 1.5.4

章 第02 线性映射
def 2.1.1 线性映射(linear transformation)

thm 2.1.1


thm 2.1.2

thm 2.1.3






lemma 2.1.1

thm 2.1.4



def 2.2.1 坐标化


thm 2.2.1

thm 2.2.1 cor 1
def 2.2.2 同构(isomorphism)

def 2.2.3 坐标同构函数
thm 2.2.2

thm 2.2.3

lemma 2.2.1

def 2.2.4 (基底)转移矩阵、坐标变换矩阵

thm 2.2.4


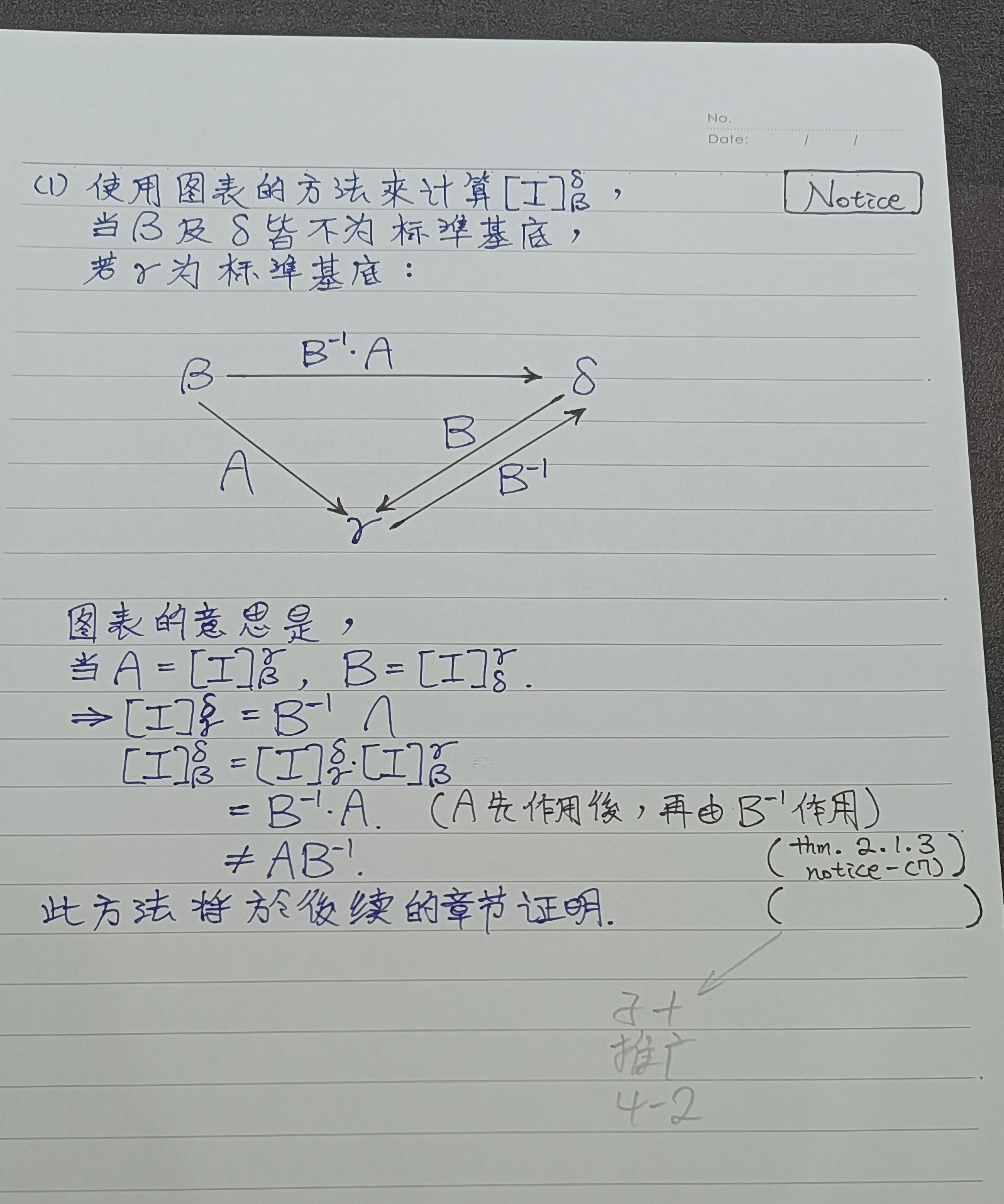
def 2.3.1 (线性映射相对于基底的)矩阵表示法

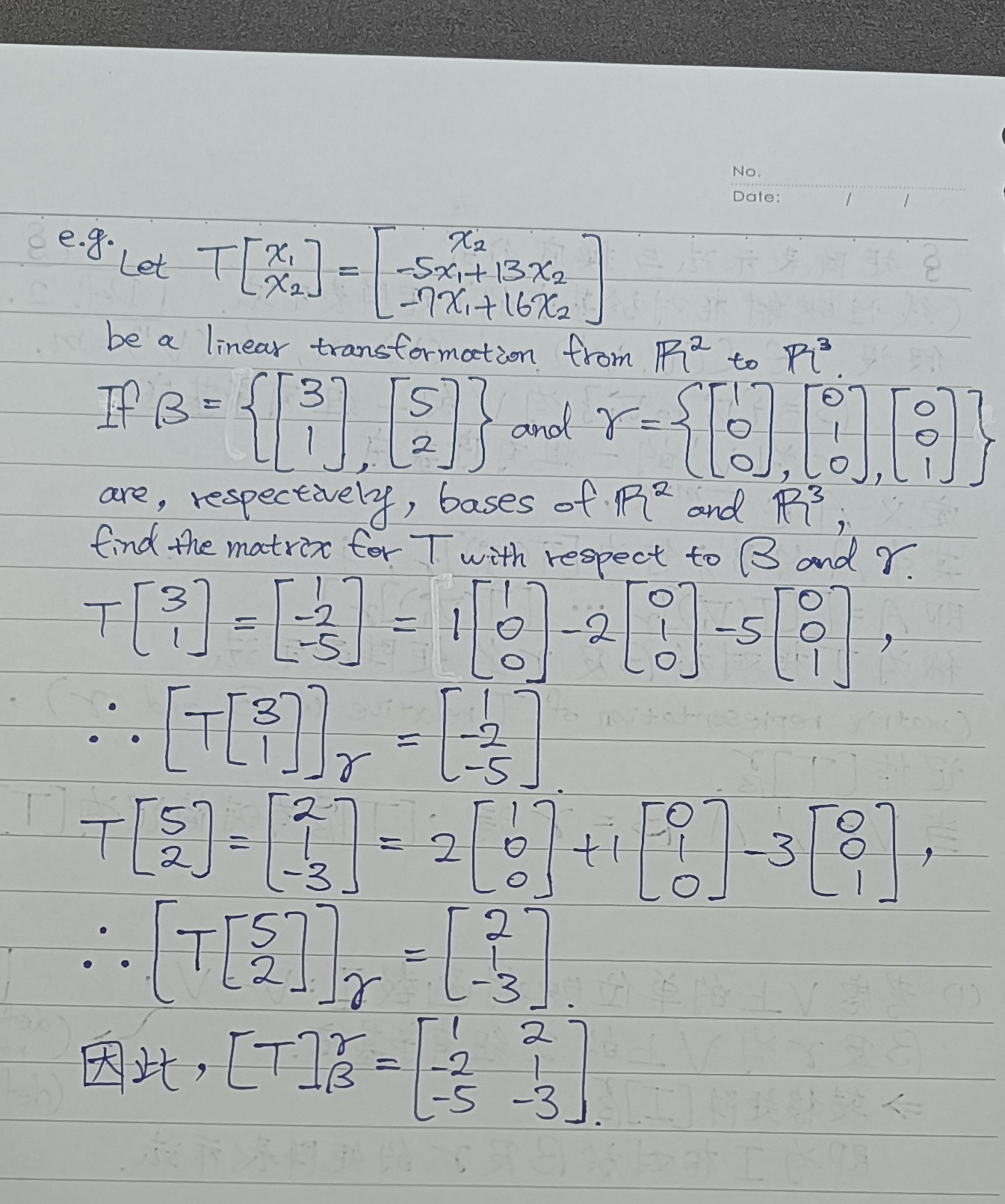
thm 2.3.1

thm 2.3.2

lemma 2.3.1
thm 2.3.3



thm 2.3.4



def 2.4.1 直像、反像
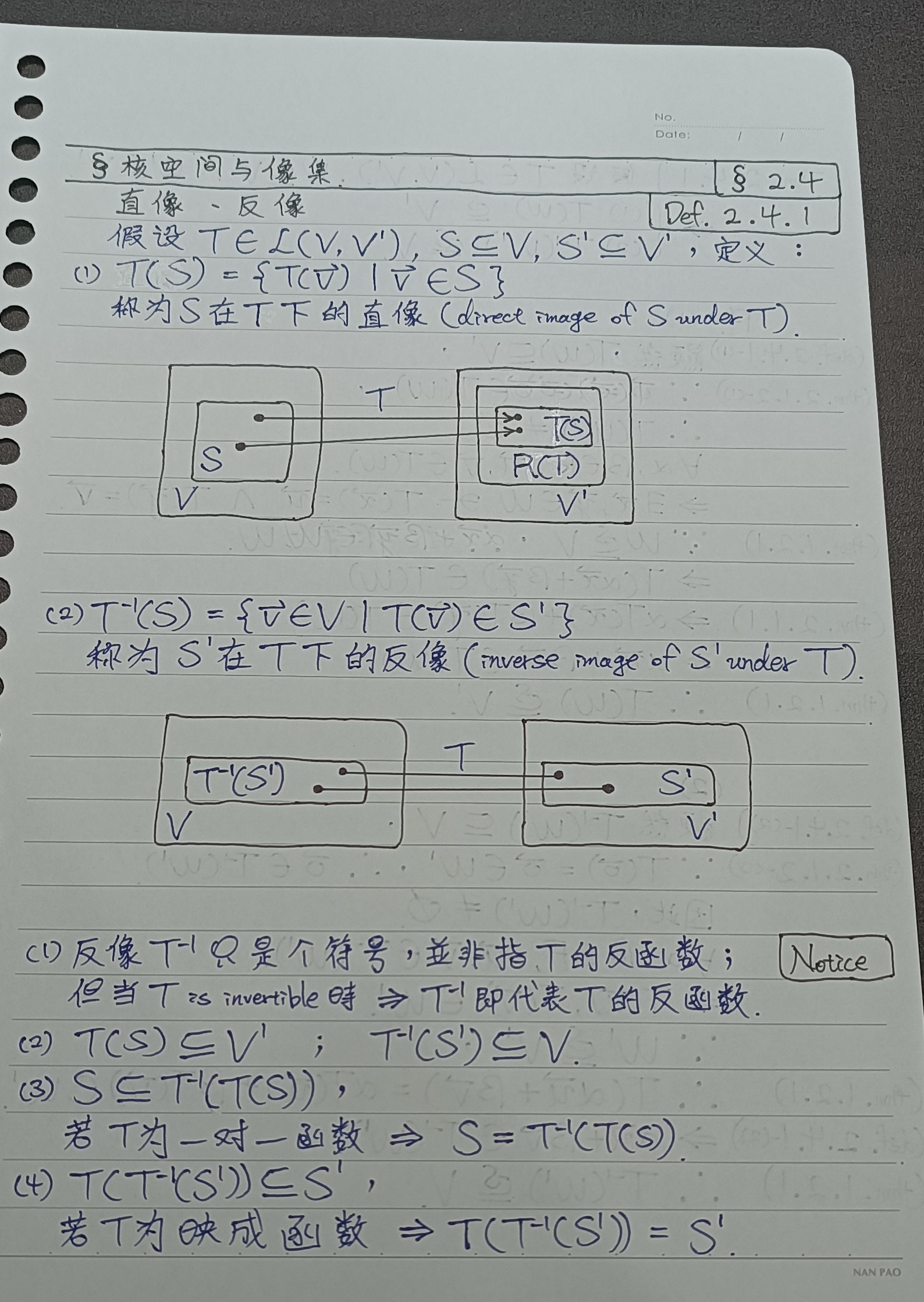
thm 2.4.1

def 2.4.2 核空间、像
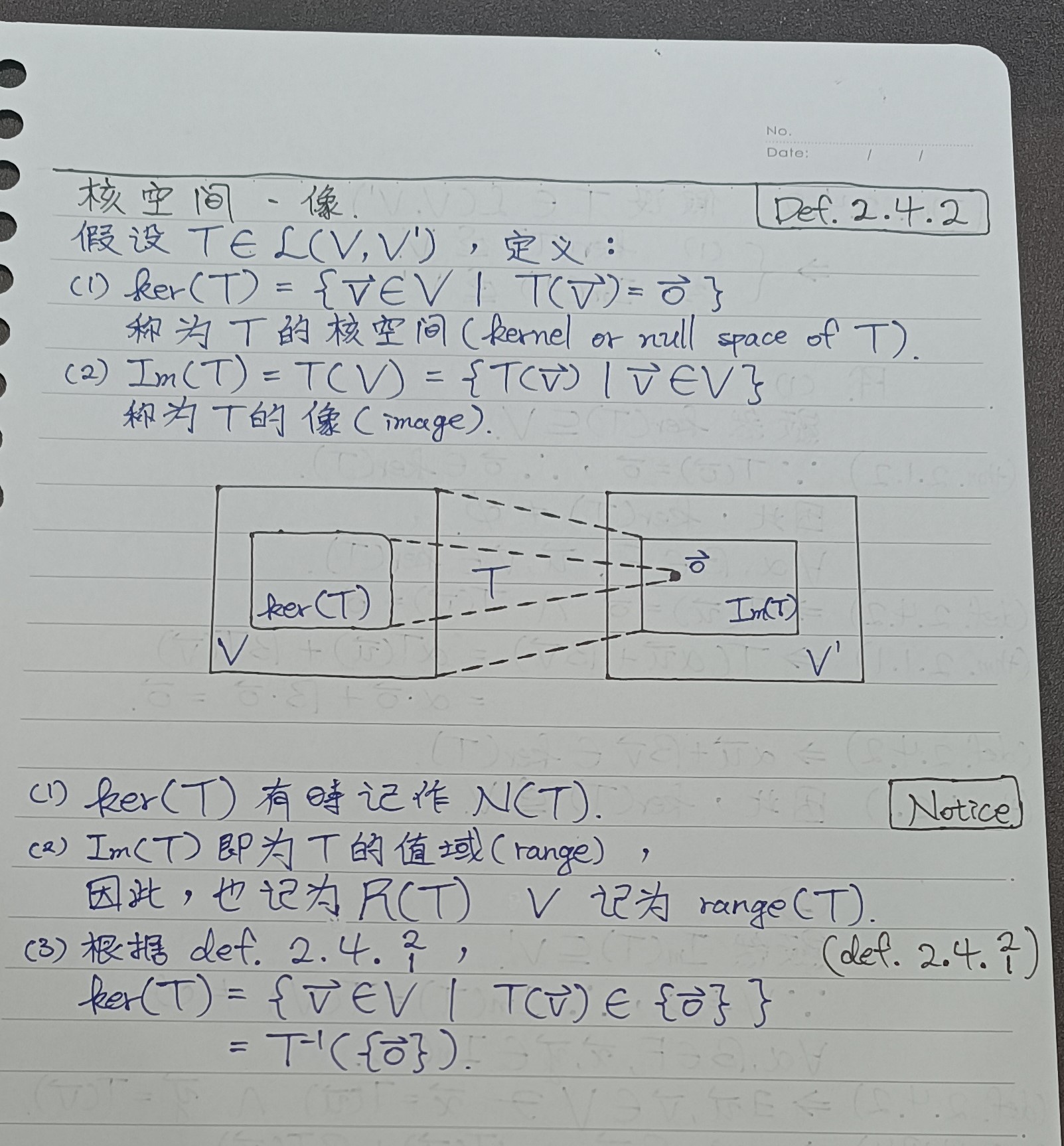
thm 2.4.2

def 2.4.3 核数(nullity)、秩(rank)
thm 2.4.3


thm 2.4.4


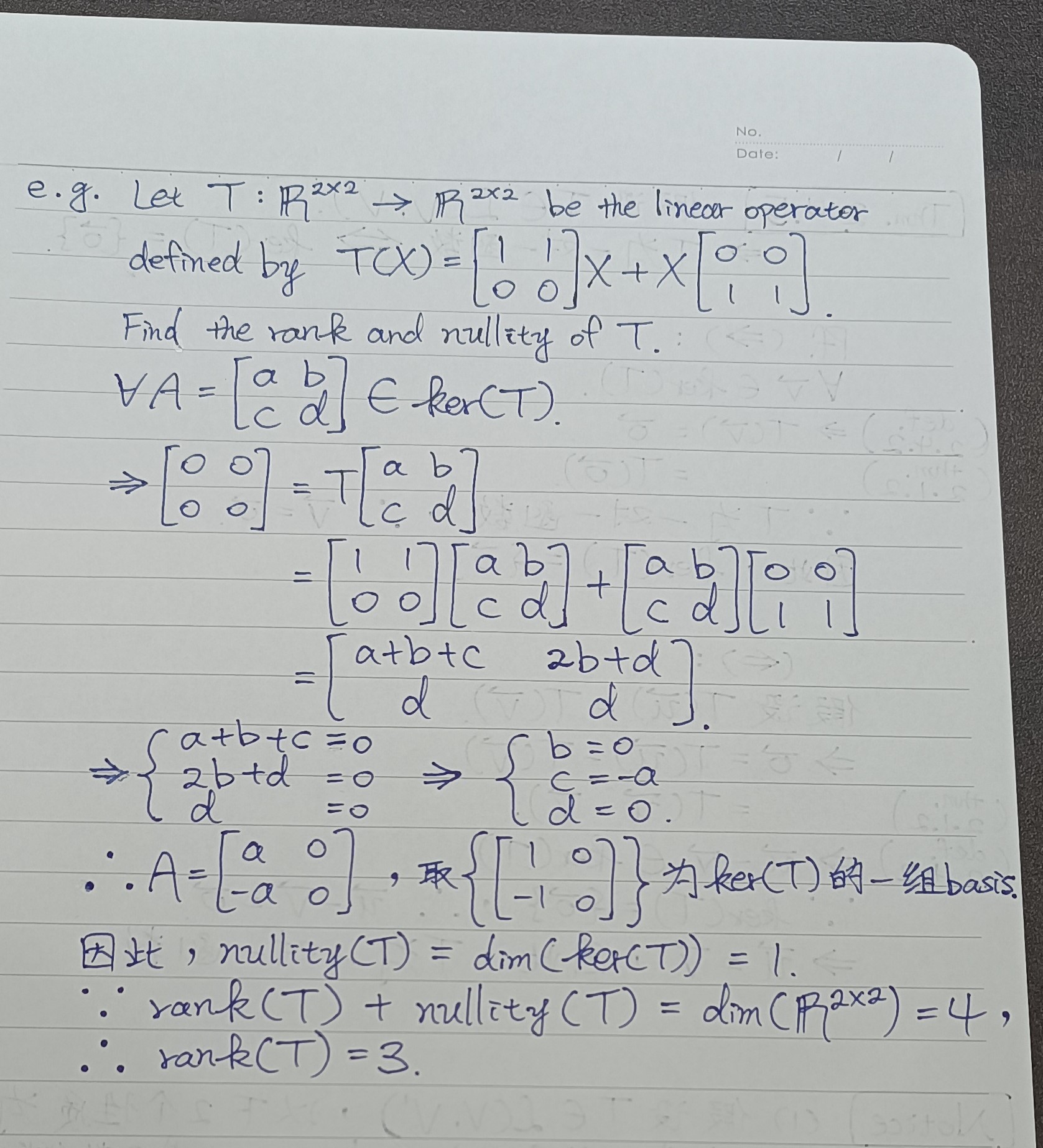
thm 2.4.5


thm 2.4.6


thm 2.4.7


thm 2.4.8
def 2.4.4 保相依、保独立、保生成

thm 2.4.9

thm 2.4.10

thm 2.4.11

thm 2.4.12



thm 2.4.13


def 2.5.1 列秩、行秩
thm 2.5.1

章 第03 矩阵与线性方程组
def 3.1 矩阵

def 3.1.1 矩阵的基本名词——(特殊矩阵)


def 3.1.2 (矩阵运算)矩阵加减法、纯量积
def 3.1.3 (矩阵运算)矩阵乘法

thm 3.1.1
thm 3.1.2








thm 3.1.3

def 3.1.4 矩阵相等
def 3.1.5 矩阵转置

thm 3.1.4 矩阵转置的运算性质

def 3.1.6 与矩阵转置相关的特殊矩阵

thm 3.1.5

def 3.1.7 迹数(trace)
thm 3.1.6


def 3.2.1 左逆矩阵、右逆矩阵

def 3.2.2 逆矩阵(inverse matrix)

thm 3.2.1
thm 3.2.2
thm 3.2.3

thm 3.2.3 cor 1

thm 3.2.4

def 3.2.3 方阵多项式
thm 3.2.5

def 3.3.1 基本列运算有三种型态

def 3.3.2 列基本矩阵(row elementary matrix)

thm 3.3.1

thm 3.3.2

def 3.3.3 列等价、等价关系(equivalence relation)

thm 3.3.3


def 3.4.1 线性联立方程组:一种线性系统


thm 3.4.1
def 3.4.2 列梯形矩阵(r.e.f.)、列简化梯形矩阵(r.r.e.f.)

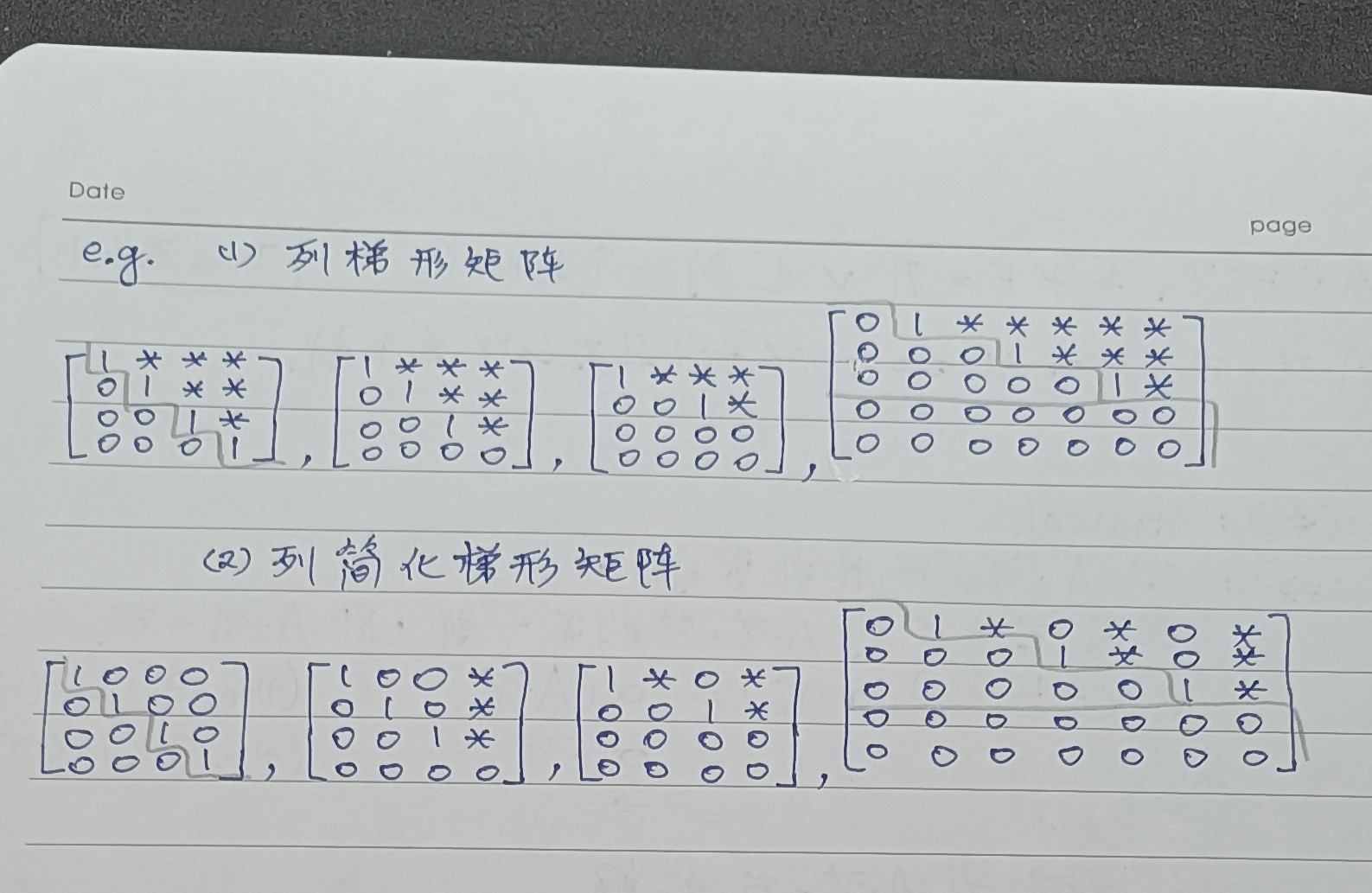

def 3.4.3 Gaussian、Gauss-Jordan消去法



notice 3.4.3.2


thm 3.4.2

thm 3.4.3

thm 3.4.4

def 3.4.4 秩(rank)


thm 3.4.5

lemma 3.5.1

thm 3.5.1

求逆矩阵的第一种方法

thm 3.5.2
thm 3.5.3

thm 3.5.4


def 3.6.1 LU-decomposition(LU-分解)



def 3.6.2 LDU-分解

def 3.6.3 排列矩阵(将单位矩阵做若干次列交换而得的矩阵)
thm 3.6.1




def 3.7.1 基本行运算有三种形态

def 3.7.2 行基本矩阵(column elementary matrix)
def 3.7.3 行等价

thm 3.7.1
thm 3.7.2
thm 3.7.3

thm 3.7.4

章 第04 Determinant——对矩阵之性质(具决定因素的)行列式
def 4.1.1 二阶行列式

thm 4.1.1

def 4.2.1 (高)n阶行列式

def 4.2.2 余因子(cofactor)
thm 4.2.1


thm 4.2.2 The Laplace Expansion Theorem


thm 4.2.3

thm 4.3.1

lemma 4.3.1

thm 4.3.2

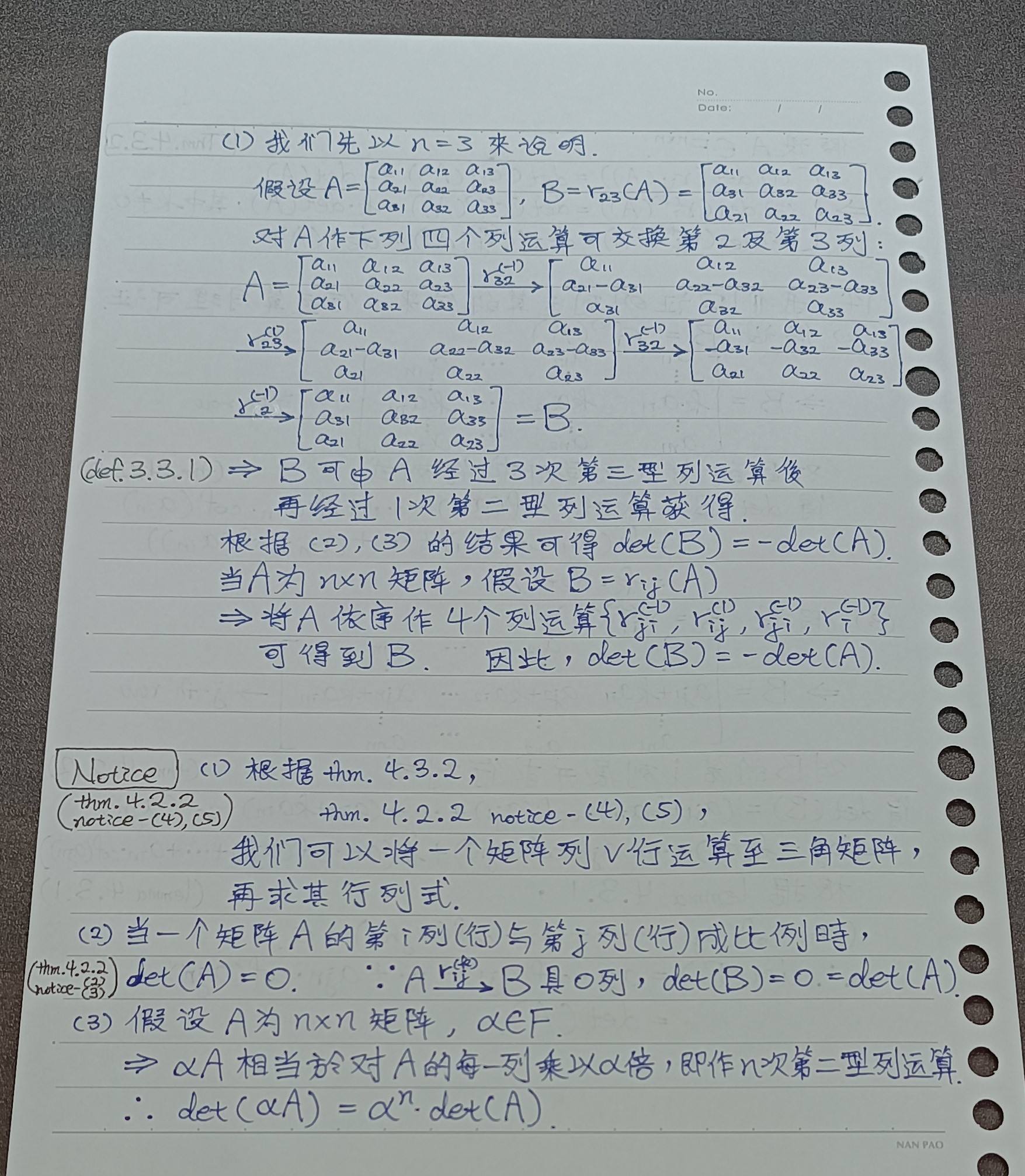
thm 4.3.3

lemma 4.3.2
lemma 4.3.3

thm 4.3.4
thm 4.3.5


thm 4.3.6

thm 4.3.7

Special 4.3.1


thm 4.3.8


def 4.4.1 古典伴随矩阵(classical adjoint matrix)

thm 4.4.1

thm 4.4.2
求逆矩阵的第二种方法

lemma 4.4.1


thm 4.4.3

thm 4.4.4